Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
Tags
- java
- 웹개발기초
- 윤곽선검출
- 딥러닝
- 컴퓨터비전
- 확인문제
- 백준괄호
- 이것이자바다
- 백준가운데를말해요
- 스파르타코딩클럽
- 이것이자바다확인문제
- 백준평범한배낭
- 이것이자바다9장
- BOJ
- 2019카카오코테
- 냅색알고리즘
- KT포트포워딩
- 백준10828
- 카카오코테
- 코딩테스트실력진단
- 코테
- 백준스택
- 백준9012
- 합성곱연산
- 백준온라인저지
- 백준
- 가운데를말해요
- 운영체제
- 코드트리
- BOJ1655
Archives
- Today
- Total
코딩하는 락커
4. 네트워크 계층 4 본문
거리 벡터(Distance-Vector, DV) 라우팅 알고리즘
- 거리 벡터 알고리즘의 특징
- 분산적 : 각 노드는 하나나 그 이상의 직접 연결된 이웃으로부터 정보를 받고, 계산을 수행하며, 계산된 결과를 다시 그 이웃들에게 배포함.
- 반복적: 이웃끼리 더 이상 정보를 교환하지 않아도 될 때까지 프로세스가 지속됨.
- 비동기적: 모든 노드가 정확히 맞물려 동작할 필요가 없음.
- 최소 비용 경로의 비용들 사이의 관계
- dx(y): 노드 x로부터 노드 y까지의 최소 비용 경로
- 벨만-포드(bellman-ford) 알고리즘
- dx(y) = MINv{c(x,v) + dv(y)}
- c(x,v): x에서 이웃한 노드인 v까지 가는데 걸리는 비용
- dv(y): v에서 y까지 가는데 걸리는 비용
- x에서 y로 이동하는 최소 비용은 x의 모든 이웃노드 v에 대해 계산된 c(x,v) + dv(y)의 최소값이 됨.
- dx(y): 노드 x로부터 노드 y까지의 최소 비용 경로
- DV 알고리즘의 아이디어
- 출발지 노드를 x라고 가정.
- Dx = [Dx(y): y in N]
- 노드 x로부터 이웃한 모든 노드 집합 N의 노드들 y까지의 비용 추정값의 벡터.
- DV알고리즘으로 각 노드 x는 다음과 같은 라우팅 정보를 유지함
- 각 이웃 노드 v 중에서 x에 직접 접속된 이웃 노드까지의 비용 c(x,y)
- 노드 x의 거리 벡터, 즉 x로부터 N에 있는 모든 목적지 y로부터의 비용 예측값을 포함하는 벡터 Dx = [Dx(y): y in N]
- 이웃 노드들의 거리 벡터들, 즉 v가 x의 이웃이라고 하면 벡터 Dv = [Dv(y): y in N]
- 벨만 포트 방식을 통해 자신의 거리 벡터 업데이트
- Dx(y) = MINy{c(x,)v} + Dv(y)}
- 만약 업데이트로 인해 노드 x의 거리 벡터가 변경되면, x는 수정된 거리 벡터를 x의 이웃들에게 보냄.
- 그에 따라 이웃들도 자신의 거리 벡터 수정
거리 벡터 알고리즘
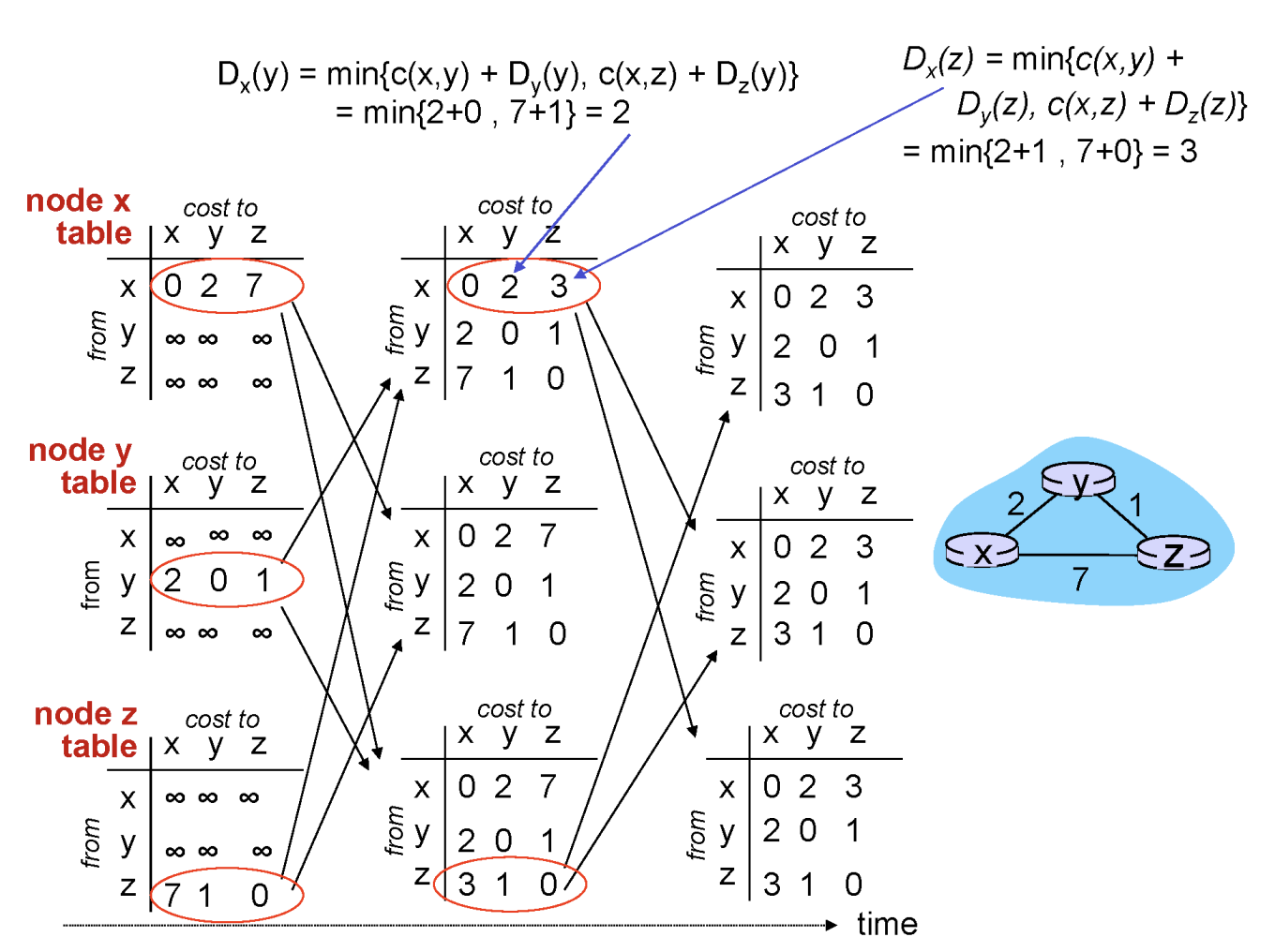
- 최초 라우팅 테이블 초기화
- 위 그림 가장 왼쪽 열 (세 개 노드 각각).
- 초기화 이후
- 각 노드는 자신의 두 이웃 각각에게 자신의 거리 벡터를 보냄 (그림 테이블들의 첫번째 열에서 두번째 열로 가는 화살표로 표현).
- 노드 x는 자신의 거리 벡터 Dx = [0,2,7]을 노드 y,z에게 보냄.
- 노드 x는 노드 y, 노드 z로부터 업데이트 된 거리 벡터 수신.
- 계산
- Dx(x) = 0
- Dx(y) = MIN{c(x,y)+Dy(y), c(x,z)+Dz(y)} = MIN{2+0, 7+1} = 2
- Dx(z) = MIN{c(x,y)+Dy(z), c(x,z)+Dz(z)} = MIN{2+1, 7+0} = 3
- 거리 벡터가 Dx = [0,2,7]에서 Dx = [0,2,3]으로 업데이트 됨
- 업데이트 이후
- 거리 벡터가 된 노드들 자신의 두 이웃 각각에게 자신의 거리 벡터를 보냄 (그림 테이블들의 두번째 열에서 세번째 열로 가는 화살표로 표현).
- 노드 x는 자신의 거리 벡터 Dx = [0,2,3]을 노드 y,z에게 보냄.
- 노드 x는 노드 z로부터 업데이트 된 거리 벡터 수신 (y는 변경되지 않았으므로 보내지 않음).
- 계산
- ...
- 위 과정을 더 이상 갱신 메시지가 없을 때까지 반복
거리 벡터 알고리즘: 링크 비용 변경과 링크 고장
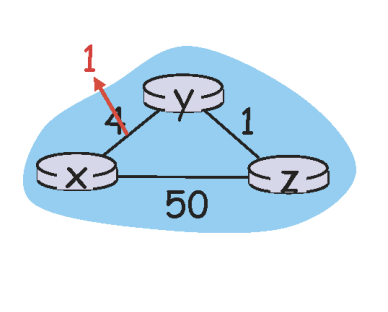
- 링크 비용 변경
- 시각 t0에 y가 링크 비용 변화 감지.
- 자신의 벡터 업데이트. Dy= [4, 0, 1] -> Dy = [1, 0, 1]
- 변경값 이웃에게 알림.
- 시각 t1에 z는 y로부터 업데이트 정보 수신.
- 자신의 벡터 업데이트. Dz = [5, 1, 0] -> Dz = [2, 1, 0]
- 변경값 이웃에게 알림
- 시각 t2에 y는 z로부터 업데이트 정보 수신
- 자신의 벡터 업데이트. Dy = [1, 0, 1] -> Dy = [1, 0, 1]
- 변경된 값 없으므로 아무런 메시지 보내지 않음.
- 시각 t0에 y가 링크 비용 변화 감지.
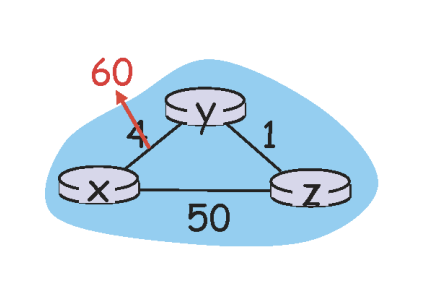
- 링크 고장
- 링크 비용 변경 전 Dy(x) = 4, Dy(z) = 1, Dz(y) = 1, Dz(x) = 5라는 값을 갖고 있음
- 시각 t0에 y가 링크 비용 변화 감지.
- 비용 업데이트. Dy(x) = 4 -> Dy(x) = 60
- Dy(x) = MIN{c(y,x)+Dx(x), c(y,z)+Dz(x)} = MIN{60+0, 1+5}
- 위 비용은 잘못되었음.
- 그러나 노드 y가 가지고 있는 유일한 정보는 x까지 직접 가는 비용은 60이고 z가 가장 최근에 y에게 x에 도착하려면 5까지비 비용이 필요하다고 말했던 사실임.
- 따라서 y는 z가 비용 5로 x에게 도달할 수 있을 것이라고 예상하고 z를 통해 x에 도달하는 경로를 말함.
- Dy= [4, 0, 1] -> Dy = [5, 0, 1]
- 변경값 이웃에게 알림.
- 시각 t1에 z는 y로부터 업데이트 정보 수신.
- 비용 업데이트. Dy(x) = 4 -> Dy(x) = 6
- 자신의 벡터 업데이트. Dz = [5, 1, 0] -> Dz = [7, 1, 0]
- 변경값 이웃에게 알림
- 시각 t2에 y는 z로부터 업데이트 정보 수신
- 자신의 벡터 업데이트. Dy = [6, 0, 1] -> Dy = [8, 0, 1]
- 변경값 이웃에게 알림
- 시간 t3에 z는 y로부터 업데이트 정보 수신
- ...
- 위 루프 z의 y를 통한 경로 비용 계산값이 50보다 커질 때 까지 이 루프 반복(44번).
- 이 문제를 무한 계수 문제(count-to-infinity problem)이라고 부름.
거리 벡터 알고리즘: 포이즌 리버스 추가
- 포이즌 리버스(poisoned reverse)
- 만약 z가 y를 통해서 목적지 x로 가는 경로 설정을 했다면
- z는 y에게 x까지의 거리가 무한대라고 알림
- 포이즌 리버스를 적용하면 y는 z에게 x로 가는 경로가 없다고 믿으므로 y는 z를 통해 x로 가는 경로를 시도하지 않음.
- 포이즌 리버스를 통한 무한 계수 문제 해결
- 링크 고장
- 링크 비용 변경 전 Dy(x) = 4, Dy(z) = 1, Dz(y) = 1, Dz(x) = 무한대라는 값을 갖고 있음
- 시각 t0에 y가 링크 비용 변화 감지.
- 비용 업데이트. Dy(x) = 4 -> Dy(x) = 60
- Dy(x) = MIN{c(y,x)+Dx(x), c(y,z)+Dz(x)} = MIN{60+0, 1+무한대}
- 무한대보다는 60이 작으므로 60선택
- Dy= [4, 0, 1] -> Dy = [60, 0, 1]
- 변경값 이웃에게 알림.
- 시각 t1에 z는 y로부터 업데이트 정보 수신.
- 비용 업데이트. Dy(x) = 4 -> Dy(x) = 60
- 자신의 벡터 업데이트. Dz = [5, 1, 0] -> Dz = [50, 1, 0]
- 변경값 이웃에게 알림
- 시각 t2에 y는 z로부터 업데이트 정보 수신
- 자신의 벡터 업데이트. Dy = [60, 0, 1] -> Dy = [51, 0, 1]
- 변경값 이웃에게 알림
- 이로써 무한 계수 문제 해결.
- 그러나 직접 이웃한 두 개의 노드가 아닌 세 개 이상의 노드를 포함한 루프는 포이즌 리버스로 감지할 수 없음.
'🌐 네트워크' 카테고리의 다른 글
| 5. 링크 계층 1 (0) | 2022.04.25 |
|---|---|
| 4. 네트워크 계층 5 (0) | 2022.04.19 |
| 4. 네트워크 계층 3 (0) | 2022.04.18 |
| 4. 네트워크 계층 2 (0) | 2022.04.12 |
| 4. 네트워크 계층 1 (0) | 2022.04.11 |
Comments



