| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 백준스택
- 백준평범한배낭
- KT포트포워딩
- 코드트리
- 가운데를말해요
- java
- 백준괄호
- 윤곽선검출
- 이것이자바다확인문제
- 카카오코테
- 스파르타코딩클럽
- 확인문제
- 백준10828
- 이것이자바다9장
- 컴퓨터비전
- BOJ1655
- 백준가운데를말해요
- 딥러닝
- 웹개발기초
- 합성곱연산
- 냅색알고리즘
- 코테
- 백준
- BOJ
- 코딩테스트실력진단
- 백준온라인저지
- 2019카카오코테
- 백준9012
- 이것이자바다
- 운영체제
- Today
- Total
코딩하는 락커
[BOJ 20057] 마법사 상어와 토네이도 본문
마법사 상어가 토네이도를 배웠고, 오늘은 토네이도를 크기가 N×N인 격자로 나누어진 모래밭에서 연습하려고 한다. 위치 (r, c)는 격자의 r행 c열을 의미하고, A[r][c]는 (r, c)에 있는 모래의 양을 의미한다.
토네이도를 시전하면 격자의 가운데 칸부터 토네이도의 이동이 시작된다. 토네이도는 한 번에 한 칸 이동한다. 다음은 N = 7인 경우 토네이도의 이동이다.
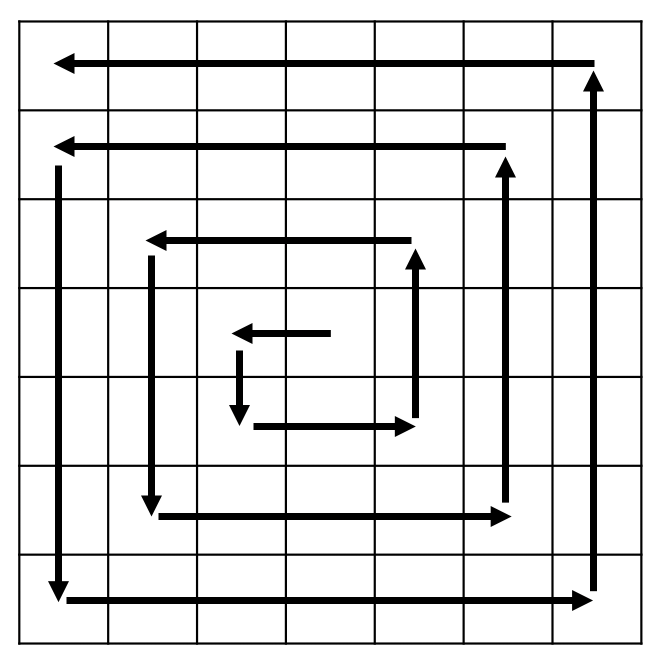
토네이도가 한 칸 이동할 때마다 모래는 다음과 같이 일정한 비율로 흩날리게 된다.
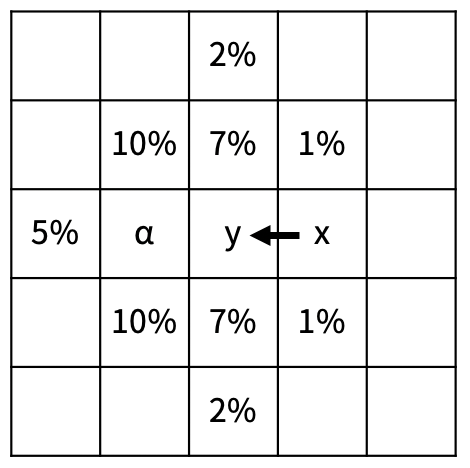
토네이도가 x에서 y로 이동하면, y의 모든 모래가 비율과 α가 적혀있는 칸으로 이동한다. 비율이 적혀있는 칸으로 이동하는 모래의 양은 y에 있는 모래의 해당 비율만큼이고, 계산에서 소수점 아래는 버린다. α로 이동하는 모래의 양은 비율이 적혀있는 칸으로 이동하지 않은 남은 모래의 양과 같다. 모래가 이미 있는 칸으로 모래가 이동하면, 모래의 양은 더해진다. 위의 그림은 토네이도가 왼쪽으로 이동할 때이고, 다른 방향으로 이동하는 경우는 위의 그림을 해당 방향으로 회전하면 된다.
토네이도는 (1, 1)까지 이동한 뒤 소멸한다. 모래가 격자의 밖으로 이동할 수도 있다. 토네이도가 소멸되었을 때, 격자의 밖으로 나간 모래의 양을 구해보자.
입력
첫째 줄에 격자의 크기 N이 주어진다. 둘째 줄부터 N개의 줄에는 격자의 각 칸에 있는 모래가 주어진다. r번째 줄에서 c번째 주어지는 정수는 A[r][c] 이다.
출력
격자의 밖으로 나간 모래의 양을 출력한다.
제한
- 3 ≤ N ≤ 499
- N은 홀수
- 0 ≤ A[r][c] ≤ 1,000
- 가운데 칸에 있는 모래의 양은 0
코드
import sys
N = int(sys.stdin.readline())
grid = list(list(map(int, sys.stdin.readline().split())) for _ in range(N))
dx, dy = [0, 1, 0, -1], [-1, 0, 1, 0]
x, y, dir, dist, cnt = N//2, N//2, 0, 1, 0
sand_dir = [
# (비율, 방향, 이동량)
[[0.01, 1, 1], [0.01, 3, 1]],
[[0.07, 1, 1], [0.07, 3, 1], [0.02, 1, 2], [0.02, 3, 2]],
[[0.1, 1, 1], [0.1, 3, 1]],
[[0.05, 0, 0]]
]
result = 0
def in_range(x, y):
return 0 <= x < N and 0 <= y < N
# 토네이도가 s_x, s_y에서 e_x, e_y로 이동한다고 할 때 모래를 계산하는 함수
def calc(s_x, s_y, e_x, e_y, dir):
global result
# e_x, e_y가 범위 밖이라면
if not in_range(e_x, e_y):
result += grid[s_x][s_y]
return
init_val = grid[e_x][e_y]
grid[e_x][e_y] = 0
# x, y는 시작 인덱스로 초기화
# total은 움직인 모래의 총량
x, y, total = s_x, s_y, 0
for i in range(4):
for rat, d, m in sand_dir[i]:
new_dir = (dir + d) % 4
new_x, new_y = x+(dx[new_dir]*m), y+(dy[new_dir]*m)
sand = int(init_val*rat)
total += sand
if not in_range(new_x, new_y): result += sand
else: grid[new_x][new_y] += sand
x, y = x+dx[dir], y+dy[dir]
# 알파값 계산
alpha = init_val - total
a_x, a_y = s_x+(dx[dir]*2), s_y+(dy[dir]*2)
if not in_range(a_x, a_y): result += alpha
else: grid[a_x][a_y] += alpha
def spread_sand(s_x, s_y, e_x, e_y, dir):
x, y = s_x, s_y
while True:
if x == e_x and y == e_y: break
new_x, new_y = x+dx[dir], y+dy[dir]
calc(x, y, new_x, new_y, dir)
x, y = new_x, new_y
for i in range(N+N-1):
if cnt == 2:
cnt = 0
dist += 1
new_x, new_y = x+(dx[dir]*dist), y+(dy[dir]*dist)
if i == N+N-2:
new_y += 1
spread_sand(x, y, new_x, new_y, dir)
x, y = new_x, new_y
dir = (dir+1) % 4
cnt += 1
print(result)풀이
생각보다 얼마 안걸렸다. 한 한시간정도~? ^^
사실 다른 것보다 문제를 이해하는데에 오래걸렸다. 처음에는 화살표의 좌표로 이동할 때 (마지막 for문에서 x,y 에서 new_x, new_y로 이동할 때) 마다 저 모래 연산이 이루어지는 줄 알았는데 그게 아니고 좌표위에서 한칸 한칸을 움직일 때마다 모래 연산을 해야하는 것이었다. (문제를 잘읽자 ..)
먼저 나는 토네이도의 이동은 가장 바깥쪽 for문에서 구현해주었다.
dist가 화살표의 크기가 1, 1, 2, 2, 3, 3, 4, 4, .. 이런식으로 커져가는 것에서 규칙을 찾아서 dist값으로 구현하였다.
dist는 저런 규칙을 갖지만 dir은 매 화살표마다 계속 변하므로 dir = (dir+1) % 4 라는 연산을 해주어 갱신해주었다.
아 그리고 i == N+N-2은 마지막 화살표가 원래는 위의 규칙에 따르면 1, 1, 2, 2, .. N-1, N-1, N 이런식으로 되어서 N이 되어야 하는데 격자 상에서 0, 0까지만 토네이도가 움직인다는 조건이 있어 이례적으로 마지막 화살표의 크기만 N에서 -1한 값이 되어서 추가해준 조건이다.
여튼 저렇게 한 x, y에서 new_x, new_y까지의 화살표의 거리를 구하게 되면 해당 화살표의 크기 만큼 모래 연산을 해주기 위해 spread_sand 함수를 호출하였다.
spread_sand 함수도 별거 없고 x,y가 s_x, s_y에서 e_x, e_y에 도달할 때까지 x+dx[dir], y+dy[dir] 연산을 해주어 new_x, new_y를 만든 뒤 x, y, new_x, new_y를 매개변수로 하여 calc함수를 호출하는 것이다.
가장 중요한 calc 함수는 어떻게 구현할지 고민을 좀 하다가 sand_dir 이라는 배열로 구현하기로 하였다.
sand_dir은 토네이도가 x에서 y로 움직일 때, 즉 내 코드에서는 spread_sand에서 calc를 호출할 때 넣어전 매개변수인 x,y에서 dir방향으로 new_x, new_y 지점으로 (calc 함수에서는 s_x, s_y, e_x, e_y이다) 토네이도가 움직일 때 모래가 흩날리는 비율, dir로부터의 방향값, 이동량을 하드코딩 해준 배열이다.
방향값은 dir에서 +1을 해준 값은 시계방향으로 90도 움직인 값이 나오고 +3을 해준 값은 시계방향으로 -90도 해준 값이 나오는 매커니즘을 사용하여 저렇게 적었다.
여기서
0 :[[0.01, 1, 1], [0.01, 3, 1]],
1: [[0.07, 1, 1], [0.07, 3, 1], [0.02, 1, 2], [0.02, 3, 2]],
2: [[0.1, 1, 1], [0.1, 3, 1]],
3: [[0.05, 0, 0]]
으로 2차원 배열로 선언한 이유는 x,y가 calc의 매개변수인 s_x,s_y 에서 e_x, e_y로 움직인다고 할 때 dir 방향으로 1칸씩 4번 움직이게 구현했기 때문이다. 즉 4번의 x+dx[dir], y+dy[dir] 의 연산을 해주어 구현했다는 뜻이다.
그리고 문제에서 구하라고 하는 값이 격자 밖으로 떨어지는 값을 구하라고 한 것이기 때문에 x+dx[dir], y+dy[dir]값인 new_x, new_y가 격자 범위 밖이라면 global로 선언한 result 변수에 더해주었고, 범위안이라면 grid[new_x][new_y]에 더해주었다.
뭔가 문제 이름 보고 쫄았는데 생가보다 할만 했던 문제였다~
'💯 코딩테스트 > [2021~] 💯 코딩테스트' 카테고리의 다른 글
| [BOJ 3085] 사탕게임 (Go 풀이) (0) | 2025.10.19 |
|---|---|
| [BOJ 27210] 신을 모시는 사당 - Python 풀이 (0) | 2023.01.14 |
| [BOJ 27211] 도넛 행성 - Python 풀이 (0) | 2023.01.14 |
| [2022 KAKAO TECH INTERNSHIP] 등산코스 정하기(118669) (0) | 2022.12.29 |
| [BOJ 17406] 배열 돌리기4 - Python 풀이 (2) | 2022.12.23 |


