| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 이것이자바다9장
- 가운데를말해요
- 백준10828
- 코드트리
- KT포트포워딩
- 백준
- 코딩테스트실력진단
- 냅색알고리즘
- java
- 카카오코테
- 합성곱연산
- 딥러닝
- 이것이자바다확인문제
- 이것이자바다
- 웹개발기초
- 백준가운데를말해요
- 운영체제
- 코테
- 백준괄호
- 2019카카오코테
- 백준평범한배낭
- 백준스택
- 윤곽선검출
- 백준9012
- BOJ
- 스파르타코딩클럽
- 백준온라인저지
- 확인문제
- BOJ1655
- 컴퓨터비전
- Today
- Total
코딩하는 락커
[Week3] 합성곱 네트워크의 한 계층 구성하기 본문
앞선 포스팅 입체형 이미지에서의 합성곱에서 구한 4 x 4 x Nc 사이즈의 결과 이미지를 합성곱 신경망 층으로 만들기 위해서 해야 할 마지막 일은 각각에 편향Bias을 곱해 주는 것이다.
이 때 Bias값은 실수여야 하며 모든 요소에 동일한 수를 더해주어야 하며 ReLU와 같은 비선형성을 적용해주어야 한다. 다른 채널의 결과 이미지도 마찬가지이다.
그리고 결과 이미지를 모두 쌓으면 비로소 신경망의 한 계층이 되는 것이다.
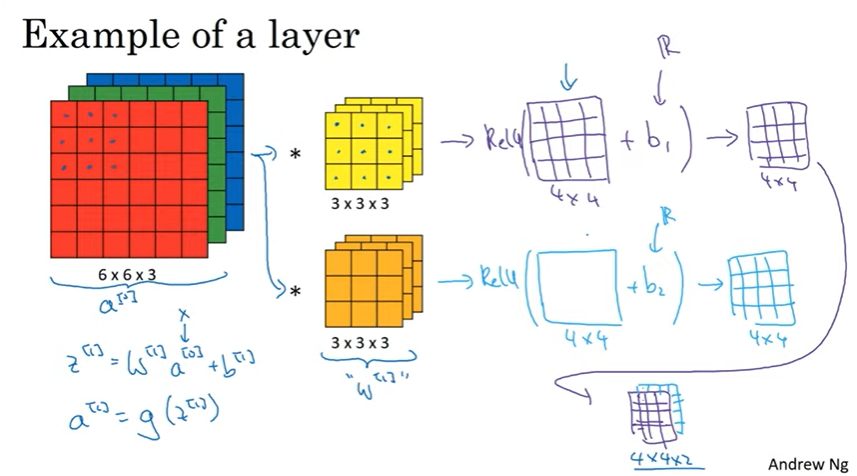
이제 합성곱이 아닌 표준 신경망의 한 계층으로 연결시켜보자.
전파의 바로 전 단계는 z[1] = w[1]a[0](=x)+b[1]에 비선형성을 적용해줌으로써 a[1]=g(z[1])를 얻는데, 여기서 a[0]는 6 x 6 x 3 사이즈의 이미지라고 볼 수 있고, 3 x 3 x 3 사이즈 필터 두 개는 w[1]과 유사한 역할을 한다고 볼 수 있다. 왜냐하면 3 x 3 x 3 = 27개의 값들을 이미지 각각의 값들에 일일이 곱해주기 때문이다.
그래서 합성곱 연산의 결과값에 Bias값을 적용해주면 구하고자 하는 z[1]과 같아지고, 그러면 6 x 6 x 3의 a[0]에서 신경망의 다음 층인 4 x 4 x 2의 a[1]이 구해지는 것이다.
이 예시에서는 가로와 세로 두 가지 특성을 가지기 때문에 4 x 4 x 2의 결과가 나온 것이지만 만약 10개의 특성을 가진다면 4 x 4 x 10의 결과가 나온다고 한다.
그리고 영상에서는 이제 연습을 해보자고 하는데....나는 안하겠다 껄껄(0_<)-☆
대신 표기법을 알아보자.
- l : l번째 계층
- f^[l] : 필터의 크기 = f^[l] x f^[l] x n_c^[l-1]
- p^[l] : 패딩의 양
- s^[l] : 스트라이드 크기
- n_H : 이미지의 높이
- n_W : 이미지의 넓이
- n_c : 채널의 수 = n_c^[l-1]

표기법이 다음과 같다고 할 때, Input값은 n_H[l-1] x n_W[l-1] x n_C[l-1]이 되며, Output값은 n_H[^l] x n_W^[l] x n_C^[l]
이다.
이전 포스팅까지 Output값은 (n+2p-f) / s +1의 절대값이었는데, 표기법을 참고하면 n_H^[l] = (n_H^[l-1] + 2p^[l] - f[l]) / s^[l] +1, n_W^[l] = (n_H^[l-1] + 2p^[l] - f[l]) / s^[l] +1의 절대값으로 나타낼 수 있다.
그리고 편향과 비선형을 적용한 뒤의 출력이 이 계층의 Activations값인 a^[l]이 되고, n_H^[l] x n_W^[l] x n_C^[l]의 크기이다.
가중치 Weight는 가중치의 개수, 즉 필터를 전부 모은 값의 합이기 때문에 필터의 값에 필터의 개수를 곱한 값인 f^[l] x f^[l] x n_c^[l-1] x n_C^[l]이 된다.
편향값 Bias는 필터마다 하나의 실수값인 편향을 가지기 때문에 n_C^[l]이며, 추후에는 (1,1,1,n_C^[l])인 4차원 행렬, 혹은 텐서로 나타낸다고 한다.
이해가 되는 것 같기도 하고 아닌 것 같기도 하다....^,^;
'[2020] 📚 DSC 겨울방학 스터디' 카테고리의 다른 글
| [Week3] CNN 예시 (0) | 2020.02.01 |
|---|---|
| [Week3] 풀링 (0) | 2020.02.01 |
| [Week3] 입체형 이미지에서의 합성곱 (0) | 2020.01.31 |
| [Week3] 스트라이드 (0) | 2020.01.24 |
| [Week3] 패딩 (0) | 2020.01.24 |




