| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 카카오코테
- 2019카카오코테
- BOJ
- 백준10828
- KT포트포워딩
- 확인문제
- 합성곱연산
- 딥러닝
- 코테
- 컴퓨터비전
- 백준9012
- 백준
- 백준스택
- 냅색알고리즘
- 가운데를말해요
- 백준가운데를말해요
- 코드트리
- 코딩테스트실력진단
- 윤곽선검출
- 백준괄호
- 이것이자바다
- 스파르타코딩클럽
- java
- 백준온라인저지
- 운영체제
- 웹개발기초
- BOJ1655
- 백준평범한배낭
- 이것이자바다9장
- 이것이자바다확인문제
- Today
- Total
코딩하는 락커
[Week3] 왜 합성곱을 사용할까요? 본문
뭔가 순서가 바뀌었다고 생각할 수도 있지만 이제 우리는 왜 신경망에서 합성곱을 사용하는 것이 유용한지에 대해 알아보자.
Fully Connected Layer 대신 합성곱 층을 사용할 때 두 가지 이점이 있다. 변수 공유와 희소 연결이다.
예를 들어 일반적인 신경망에서 32 x 32 x 3 이미지를 5 x 5 x 6 사이즈 필터로 28 x 28 x 6의 출력 이미지로 합성곱 연산을 했을 경우 32 x 32 x 3 = 3072의 유닛과 28 x 28 x 6 = 4704의 유닛을 연결하여 3072 x 4704 + 4704 = ...약 1400만개의 변수가 필요하다.
하지만 합성곱 신경망에서는 5 x 5의 필터이므로 25개의 변수를 가지고 여기에 Bias를 더하면 26개의 변수를 갖게 되고, 여기에 6개의 필터가 있으므로 필요한 변수는 5 x 5 x 3 x 6 + 6 = 456정도로 작은 수준이다.
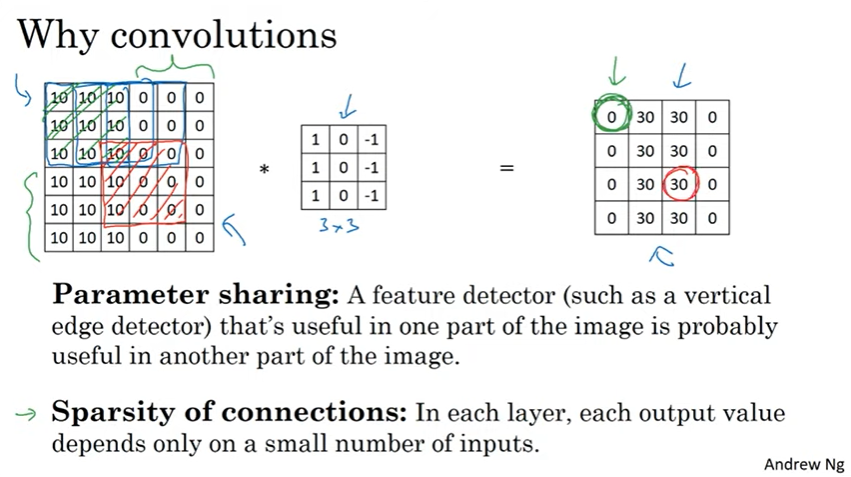
합성곱 신경망이 이렇게 적은 변수를 가지는데에는 또 두 가지 이유가 있다.
첫 번째는 변수 공유이다. 세로 윤곽선 검출기 같은 속성 검출기 관찰을 통해 발견되었다. 동일한 필터를 갖고 입력 이미지의 여러 곳에서 동일하게 사용할 수 있는 것과 같다.
두 번째는 희소 연결이다. 출력값이 이미지의 일부에만 영향을 받고 나머지 픽셀은 영향을 받지 않는다는 의미이다.
위 이미지 오른쪽 4 x 4 결과 이미지의 초록색 부분은 위 이미지 왼쪽 입력 이미지의 초록색 부분에서는 영향을 받는다는 것이다. 이 때문에 합성곱 신경망은 과적합 또한 방지할 수 있다.
또 합성곱 신경망은 이동 불변성을 알아내는 데도 효과적이라고 한다.
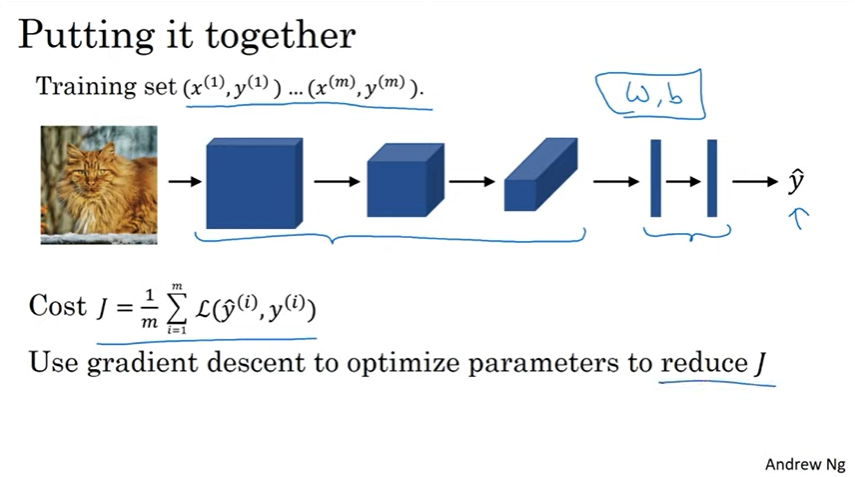
이제 하나의 신경망을 훈련시켜 보자. 고양이 이미지를 학습하는 신경망이다.
x는 이미지이고 y는 이진 레이블, 혹은 k개의 클래스 중 하나이고 합성곱 신경망 구조를 사용하여 이미지->합성곱->풀링층->완전 연결층->소프트맥스->소프트맥스의 출력값인 예측값 y의 구조를 따른다.
완전 연결층과 소프트맥스 함수는 w와 b를 갖고 변수를 설정하여 비용함수를 찾을 수 있다.
이 때 비용함수는 신경망의 훈련 세트에 대한 예측의 손실의 합을 m으로 나눈 값이다.
이 신경망을 훈련시키기 위해 경사 하강법, 모멘텀 경사 하강법, RMSprop등의 알고리증을 사용하여 비용함수 J를 줄이는 변수를 최적화 할 수 있다. 끝!
'[2020] 📚 DSC 겨울방학 스터디' 카테고리의 다른 글
| [Week4] 물체 로컬리제이션 + 특징점 탐지 (0) | 2020.02.03 |
|---|---|
| [Week3] 왜 케이스 스터디를 하나요? + 고전적인 네트워크들 (0) | 2020.02.01 |
| [Week3] CNN 예시 (0) | 2020.02.01 |
| [Week3] 풀링 (0) | 2020.02.01 |
| [Week3] 합성곱 네트워크의 한 계층 구성하기 (0) | 2020.01.31 |




