| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- java
- BOJ
- 냅색알고리즘
- 백준9012
- 백준
- 백준온라인저지
- 백준괄호
- 코드트리
- 백준가운데를말해요
- 이것이자바다확인문제
- 확인문제
- 백준평범한배낭
- 스파르타코딩클럽
- 코딩테스트실력진단
- 합성곱연산
- 코테
- 이것이자바다
- 컴퓨터비전
- 딥러닝
- BOJ1655
- 윤곽선검출
- 카카오코테
- 2019카카오코테
- KT포트포워딩
- 웹개발기초
- 백준10828
- 가운데를말해요
- 운영체제
- 백준스택
- 이것이자바다9장
- Today
- Total
코딩하는 락커
[Week3] 왜 케이스 스터디를 하나요? + 고전적인 네트워크들 본문
합성곱 신경망을 잘 구축하기 위해서는 다른 효율적인 신경망 구조의 케이스를 살펴봐야 한다. 마치 우리가 다른 사람의 코드를 살펴보며 공부하듯 말이다.
그래서 이번엔 몇몇의 대표적인 신경망에 대해 공부해도록 하겠다!
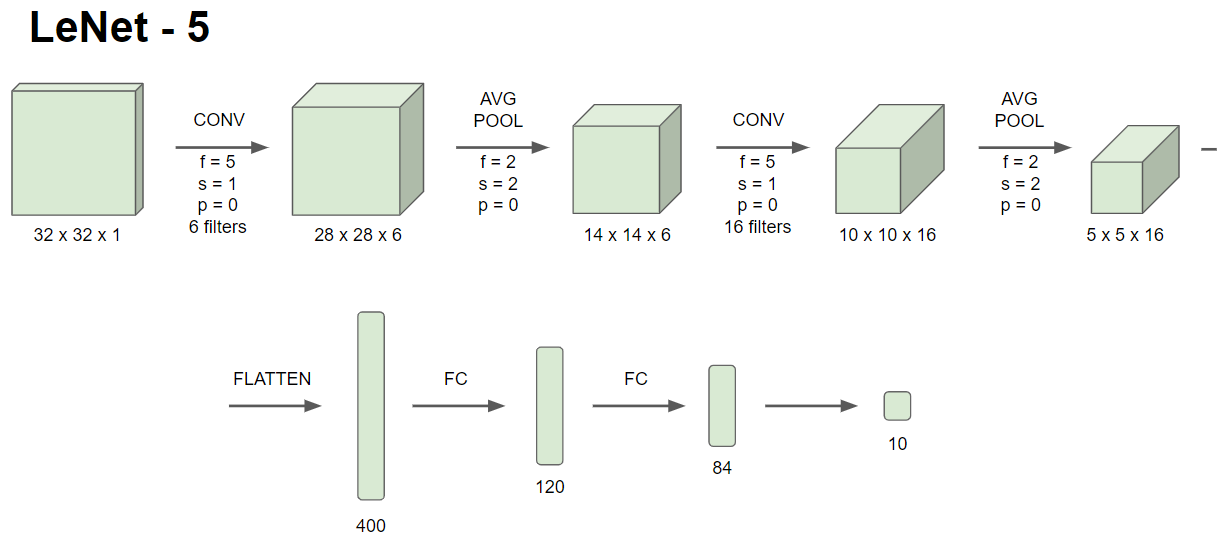
이것은 LeNet5라고 하는 손글씨의 숫자를 인식하는 목적의 신경망이다.
위 이미지와 같은 구조를 가지며, 흑백 이미지를 학습하기 때문에 32 x 32 x 1의 입력 이미지를 갖는다.
요즘에 소프트맥스를 사용하여 10개의 예측값이 나오게 하지만, LeNet5는 요즘은 잘 안쓰는 분류기를 출력층에서 사용한다고 한다.
LeNet5는 요즘 기준으로는 적은 6만개의 변수를 가지며, 논문에서는 Pooling 층 뒤에 ReLU가 아닌 Sigmoid 비선형 함수를 적용했다. 당시에는 ReLU를 적용하지 않았기 때문이다.
재밌는 점은 n_H x n_W x n_C의 신경망에서 n_C의 채널이 있다고 할 때, f x f x n_C의 필터를 통해 필터가 모든 채널을 다 살펴보게 하는 방식이 아니라 당시 컴퓨터의 연산속도 때문에 각각의 필터가 서로 다른 채널에 적용되었다고 한다. 재미없다고?....나도 알아..^_ㅠ
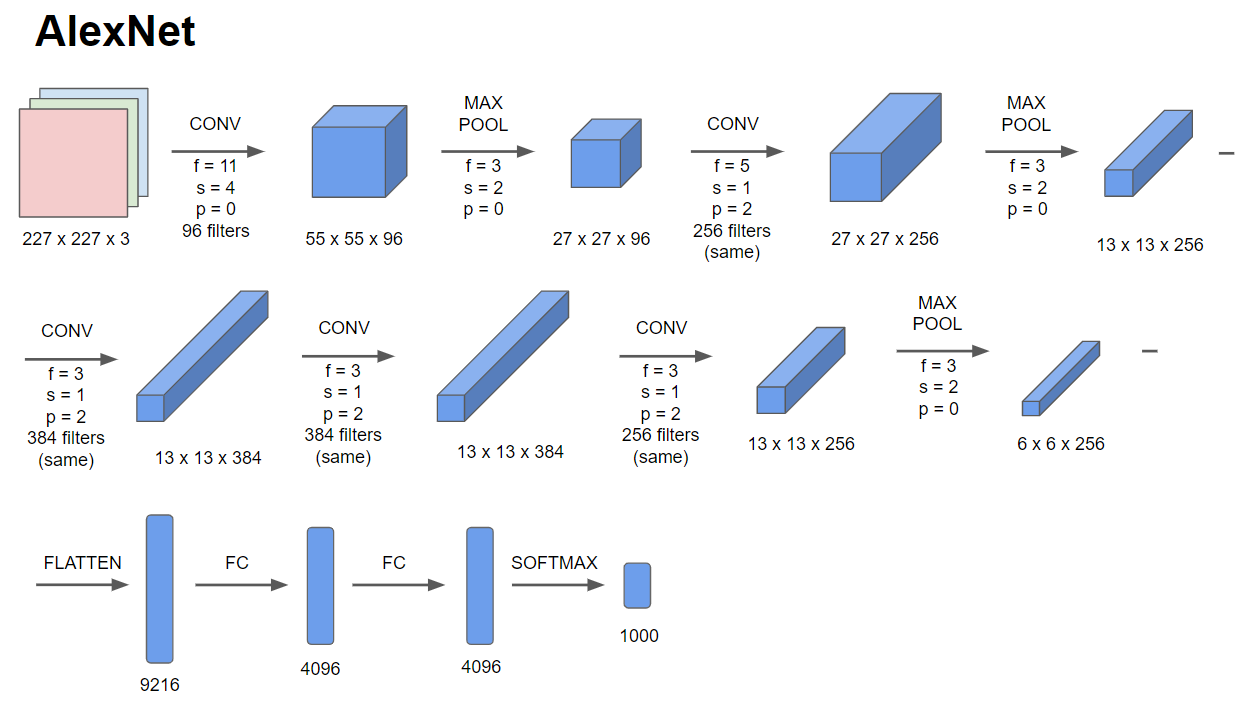
다음은 AlexNet이다. Alex Krizhevsky가 만들어서 AlexNet이라고 한다.
위 이미지와 같은 구조를 갖는다. LeNet과 구조는 비슷한데 크기는 훨씬 크다. 변수도 약 6천만개 정도이다.
또 ReLU함수를 사용한다는 점 또한 LeNet과 다르다. 그리고 당시 GPU의 성능 때문에 두 개의 GPU가 서로 소통하는 방식의 복잡한 훈련 방식을 사용했다.
AlexNet은 지역 응답 정규화LRN라고 하는 층을 갖는데, 높이와 너비가 지정된 한 지점의 모든 채널을 보고 정규화하는 것이다. 그 이유는 다음 층이 높은 활성값을 가진 뉴런을 너무 많이 원치 않기 때문이다. 하지만 이게 그렇게 효과적이진 않다고 한다.
AlexNet 논문을 통해 당시 딥러닝이 컴퓨터 비전 분야에 적용 가능하다는 것을 발견하게 되었다.
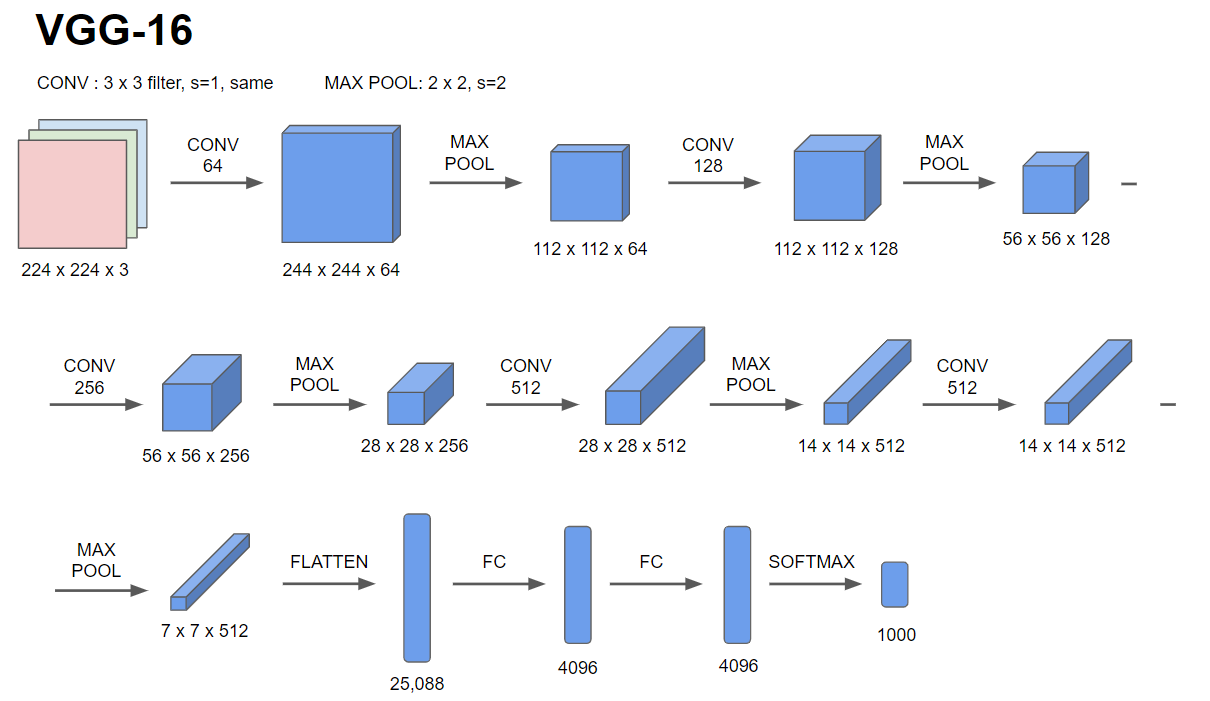
그 다음은 VGG-16 네트워크 모델이다.
이 모델에서 주목할 점은 많은 하이퍼 파라미터를 갖는 대신 합성곱에서 s=1인 3 x 3필터를 사용해 동일 합성곱을 하고 MaxPooling 층에서는 s=2인 2 x 2 필터를 사용했다는 점이다.
VGG-16 네트워크는 위 이미지와 같은 구조를 갖는다. 간결한 구조이지만 깊이는 상당히 깊다.
이름에서 16은 16개의 가중치를 의미하며 1억 3천 8백만개정도의 변수를 가진 큰 네트워크이다.
장점은 구조가 꽤 균일하다는 점이다. 몇 개의 합성곱 층 뒤에 풀링층이 크기를 줄여주고의 반복이다.
그리고 합성곱층의 필터와 개수를 살펴보면 64->128->256 ... 이런식으로 두 배씩 늘어나고 있음을 알 수 있다. 획일적인 구조이다.
단점은 역시 훈련시킬 변수가 많아 네트워크의 크기가 커진다는 점이다.
하지만 체계적인 수치의 증감이 매우 잘 짜여진 네트워크라는 것을 보여준다. 끝!
'[2020] 📚 DSC 겨울방학 스터디' 카테고리의 다른 글
| [Week4] 물체 인식 + 합성곱으로 슬라이딩 윈도 구현하기 (0) | 2020.02.06 |
|---|---|
| [Week4] 물체 로컬리제이션 + 특징점 탐지 (0) | 2020.02.03 |
| [Week3] 왜 합성곱을 사용할까요? (0) | 2020.02.01 |
| [Week3] CNN 예시 (0) | 2020.02.01 |
| [Week3] 풀링 (0) | 2020.02.01 |




